consultantsport.blogg.se

Hence, the second continuity condition of 𝑓 at 𝑥 = 𝜋 2 also holds.įinally, since this is also equal to 𝑓  𝜋 2 , we can conclude that the third continuity condition also holds and so the function 𝑓 is continuous at 𝑥 = 𝜋 2. Therefore, both the left and right limits exist and are equal to − 7, so we have shown We can then evaluate this limit by direct substitution: We can do the same for the right limit where we note that when 𝑥 > 𝜋 2, we have that 𝑓 ( 𝑥 ) = 6 2 𝑥 − 1 c o s, giving us Since this is a trigonometric expression, we can evaluate this limit by direct substitution:

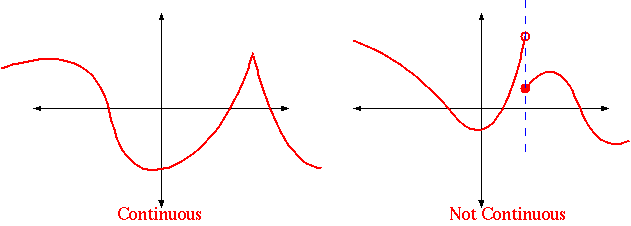
We start with the left limit and note that when 𝑥 ≤ 𝜋 2, we have 𝑓 ( 𝑥 ) = − 7 𝑥 + 7 𝑥 s i n c o s, giving us To check the second condition for continuity, we will check whether the left and right limits of 𝑓 at 𝑥 = 𝜋 2 both exist and are equal. So, the first condition for continuity at 𝑥 = 𝜋 2 holds. Therefore, 𝜋 2 is in the domain of 𝑓 and 𝑓  𝜋 2  = − 7. In our case 𝑎 = 𝜋 2, we can see from the definition of 𝑓 that l i m  →  𝑓 ( 𝑥 ) and 𝑓 ( 𝑎 ) must have the same value.s i n c o s c o s Answerįor a function 𝑓 ( 𝑥 ) to be continuous at 𝑎, we need three conditions to hold: In our first example, we will determine the continuity of a piecewise-defined function at the endpoints of its subdomains.Įxample 1: Discussing the Continuity of a Piecewise-Defined Function Involving Trigonometric Ratios at a Pointĭiscuss the continuity of the function 𝑓 at 𝑥 = 𝜋 2, given Since all three conditions hold, we have shown that 𝑓 ( 𝑥 ) = | 𝑥 | is continuous at 0. Third, we have found the values of 𝑓 ( 0 ) and l i m  →  𝑓 ( 𝑥 ) and shown that both of these are equal to the same value, 0. Therefore, the left and right limits of | 𝑥 | at 0 are equal, so Similarly, for the right limit, the values of 𝑥 are all positive, so First, when evaluating l i m  →   | 𝑥 |, the values of 𝑥 are all negative, so | 𝑥 | = − 𝑥 in this limit. We can use this to evaluate the left and right limits. We need to recall the piecewise definition of the modulus function: To evaluate this limit, we recall that we can determine whether a limit exists by checking if the left and right limits at this point both exist and are equal. Second, we need to determine l i m  →  | 𝑥 |. l i m  →  𝑓 ( 𝑥 )and 𝑓 ( 𝑎 ) must have the same value.įor example, let’s check the continuity of 𝑓 ( 𝑥 ) = | 𝑥 | at 𝑥 = 𝑎.įirst, we know that 𝑓 ( 0 ) = | 0 | = 0, so 𝑥 = 0 is in the domain of 𝑓.(This is equivalent to saying both the left and right limits of 𝑓 ( 𝑥 ) at 𝑥 = 𝑎 exist and are equal.) 𝑓 must be defined at 𝑎 ( 𝑎 is in the domain of 𝑓).To check if the function 𝑓 ( 𝑥 ) is continuous at 𝑥 = 𝑎, we need to check whether the following three conditions hold.

If f(a) is defined, continue to step 2.How To: Checking Whether a Function Is Continuous at a Point If f(a) is undefined, we need go no further.

Problem-Solving Strategy: Determining Continuity at a Point